I found the following Battleship puzzle analysis while searching Google. Mark Brader analyzes a puzzle from a 1994 issue (I'm not sure which one). His point is that there are Battlehip puzzles that make use of the "uniqueness technique".

I've quoted Mark's analysis, but modified the coordinate system to fit Fathom It!'s.

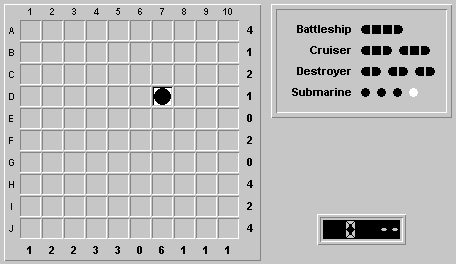
	[Ed. Filling in all obvious water results in the following line ...]
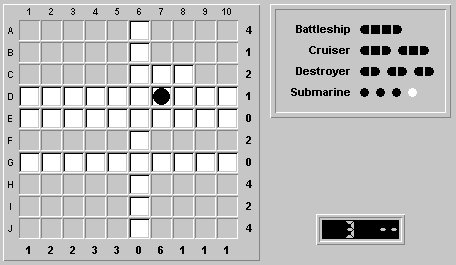
	The unoccupied row G means that no ships occupying any part of rows H-J extend into the rest of the grid. But the occupancy counts for rows H-J form a symmetrical pattern: 4, 2, 4. *If there is a unique solution, then* the arrangement of ships in those rows must have the same symmetry. Since there is only one battleship, it can't be put along row H or row J -- and hence it's along row A Also, since column 1 has an occupancy count of 1, (H,1) and (J,1) cannot both be occupied; therefore by symmetry, neither one is. Similarly in columns 8, 9, and 10. This constrains the occupied squares nicely.
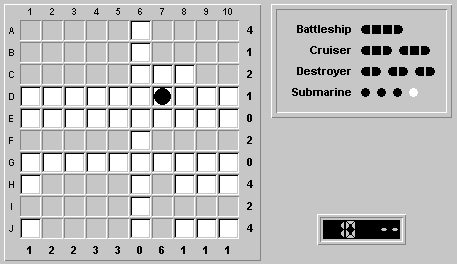
	Now, the battleship makes up all four occupied squares of row A, so there is no ship running vertically from row A. Therefore (A,7) and (B,7) are not *both* occupied. Neither are (C,7) or (E,7), being adjacent to the submarine, or (G,7), since row G is vacant. The occupancy count of 6 for column 7 then requires (H,7)-(J,7) to be occupied, i.e. with a cruiser, and (F,7) to be occupied also.
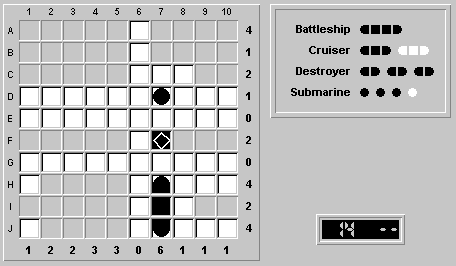
	From the occupancy counts, the only remaining places for the second cruiser are rows H and J and columns 4 and 5. We now use the symmetry one more time and deduce that it cannot be along row H or row J, as they would each have to have one. So it's along column 4 or 5... The rest is left as an exercise for the reader. [Editor: We will continue the solution in the following frames.]
	According to Mark's analysis, the remaining cruiser must reside in columns 4 or 5. There are four (4) possible placements: (A-C,4), (A-C,5), (H-J,4), and (H-J,5). We will show that three of these four placements lead to immediate contradictions: (A-C,4): Placing a cruiser here would leave no possible placement for the battleship on the board. (A-C,5): Also leaves no place for battleship on the board. (H-J,4): This would leave too many water squares on row H, with no way to get a tally count of four on the row. Therefore, the cruiser must be placed in (H-J,5).
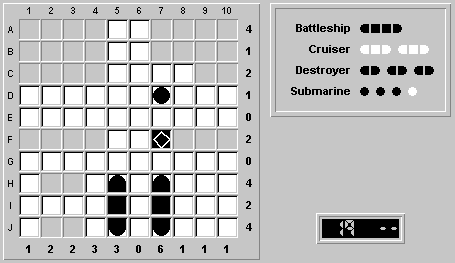
	Fill in the rest of rows H and J with segments.
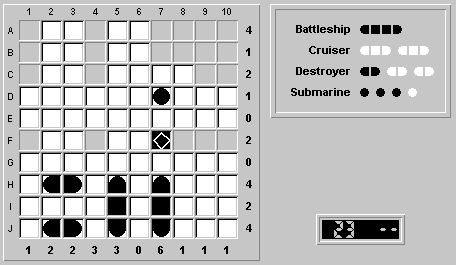
	We can now place the battleship along row A at (A,7-10).
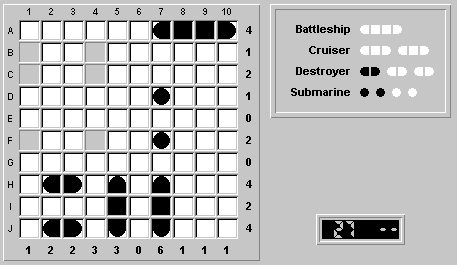
	Fill in column 4 with segments, followed by (C,1) as the final submarine and the final solution.