Thomas Snyder's excellent blog, "The Art of Puzzles", is a puzzle solver's delight, presenting Tom's original puzzles, educational insights, current events in the puzzling world, and gobs of puzzling information to boot.

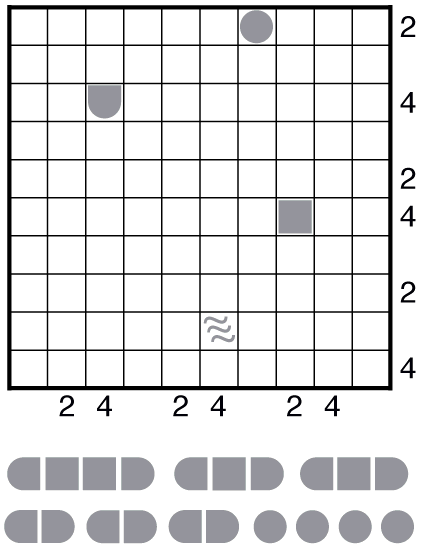
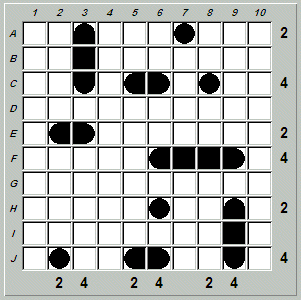
On Friday, 16 November 2012, Tom published his Friday Puzzle #177 entitled "24hour Battleships".  This is an original Battleship puzzle composition of Tom's consisting of an incomplete tally Battleship puzzle where the row and column tallies consist of the digits '2' and '4'.

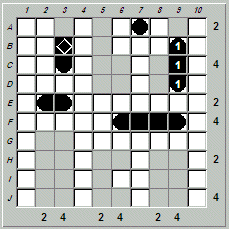
Here is the initial board, as found on the blog site:

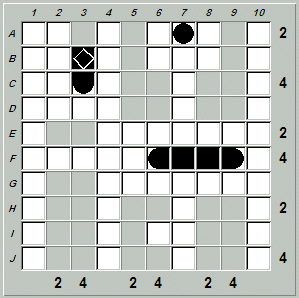
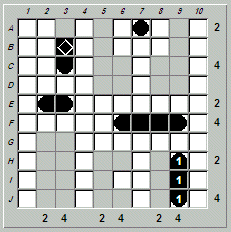
We can use Fathom It!'s "Board>Custom>Set Up New Board" menu item to solve the puzzle using its interactive interface.  In addition, we can ask Fathom It!'s built-in solver to provide hints on how to solve the puzzle.  Here is what the board looks like when loaded in Fathom It!:

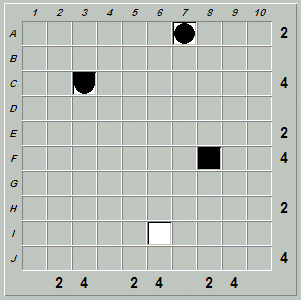
Although there are row and column tallies missing, there is enough information to solve the board.

Let's fill in all obvious segments and waters.  These include a ship segment at B3, and two segments at F7 and F9 (column 8 has a tally of two so the ship passing through F8 must be horizontal).  Inserting these segments and filling in all obvious waters gives us:

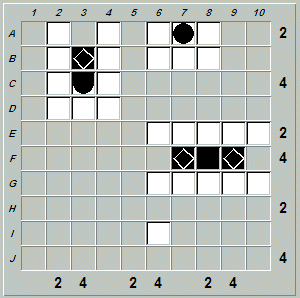
The next insight involves a common strategy often used when solving incomplete tally Battleship puzzles.

• We know that the ship fleet consists of a total of twenty (20) ship segments (one battleship, two cruisers, etc.).  This means that the sum of all column tallies, both those shown as well as those not shown, must equal twenty.
• In our puzzle we are given six (6) column tallies totally 18.  That means there are two (2) ship segments to be found in the columns without shown tallies.
• Column 7 is a column without a shown tally that has two ship segments within the column.
• We have accounted for all segments in the puzzle, which means that columns 1, 4, and 10 consist entirely of water.

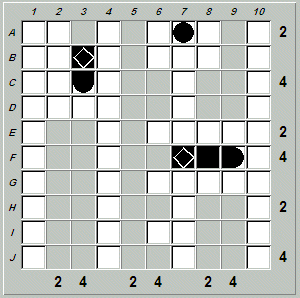
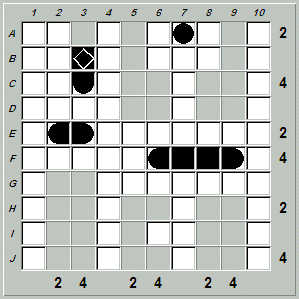
There is only one place the battleship can be placed, and that's F5-F9:

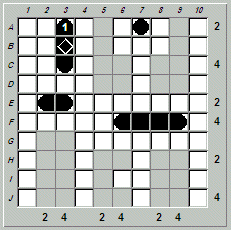
Filling in the obvious destroyer at E2-E3 gives:

The next strategy used essentially solves the puzzle for us.  We need to locate two cruisers (i.e., ships with three segments).  In how many locations can we place a cruiser?  At first glance there are four possible candidates for placing a cruiser:

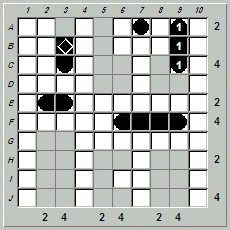A3-C3	A9-C9	B9-D9	H9-J9

On closer inspection we can rule out placing the cruiser at B9-D9 because it would violate the fact mentioned above that there are only two ship segments in unmarked rows.  If the cruiser were placed at B9-D9, there would be three (3) ship segments in unmarked rows:

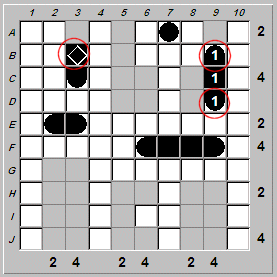
In addition, placements A3-C3 and A9-C9 are mutually exclusive.  They cannot both be used because that would place three (3) ship segments in row A, which can only accept two (2) segments.

Furthermore, placements A9-C9 and H9-J9 are mutually exclusive because the column allows only four (4) ship segments.

Therefore there is only one way to place the two cruisers on the board at the same time: A3-C3 and H9-J9.  This gives us:

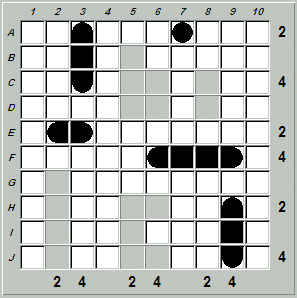
Filling in the remaining segments in row C, followed by rows J and H, gives the final solution:

Return to Board Analyses and Solutions

 Created: 17 November 2012