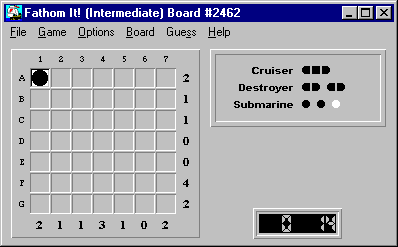
Here's the initial board:

Finalizing any obvious water square (e.g.,. (A,2) as water) gives us the following:

Let's examine row G and ask ourselves "which squares in row G can be ship segments?".

• A ship segment in either (G,2) or (G,3) would turn three squares in row F into water. This would leave three unknown squares, too few to account for a row tally of four.
• A ship segment in (G,4) would make it impossible to place a cruiser anywhere on the board:
  
  
  

Therefore, the two ships segments in row G must be placed in two of the following three squares: (G,1), (G,5) and (G,7). They cannot be in both columns 1 and 5, as this would close off row F:

So (G,7) must contain a segment:

Whichever of the squares (G,1) or (G,5) has the remaining ship segment, the cruiser will be horizontally positioned along row F.  This is because, in either case, row F will have exactly four remaining squares, all of which will have to be ship segments.

Ship segment at (G,1)	Ship segment at (G,5)

In either case, square (F,3) is a ship segment:

Because the cruiser must be positioned horizontally along row F, it cannot be placed vertically at (A,4) - (C,4). With column 4's tally of three, this means (F,4) is a ship segment:

Because row G has a tally of two, (G,1) must be a ship segment, which forces the solution:

Return to Board Analyses and Solutions