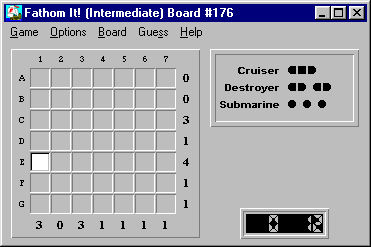
Here's the initial board:
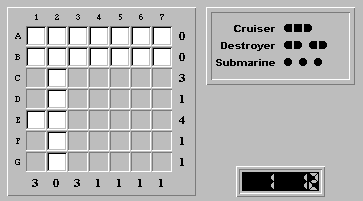
Finalizing the obvious water squares gives:
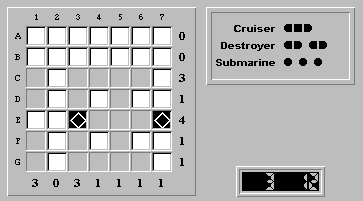
We begin our analysis by examining row E, with a row tally of four. Since there are five unknown squares on row E, the row will have exactly one water square. Where can that water square be placed? It cannot be placed at (E,3), as this would force a four-segment ship along row E (this puzzle board does not contain any four-segment ships). Using the same argument, the water cannot be placed at (E,7). Therefore, both of these squares must be ship segments:
Shmuel's following insight allows us to place two ship segments at (C,1) and (C,3).
Take a good look at the area between rows C-to-G, and columns 1-to-3:
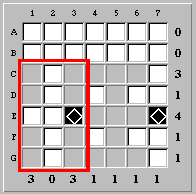
Column tallies 1 and 3 tell us that the area must have six ship segments, one of which is (E,3). So there are five more ship segments to place.
However, rows D, F, and G have row tallies of one. This means that these rows can contribute at most one ship segment to the designated area, accounting for three ship segments. Therefore, row C in the designated area must contribute at least (or exactly!) two ship segments. In other words, (C,1) and (C,3) must be ship segments:
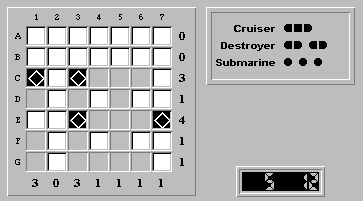
This
method of cross-checking row and column tallies is a very valuable one. It occurs frequently when solving Fathom It! boards, and is worth keeping in your "bag-o-tricks".
[Editor: Shmuel's observations end at this point. The following solution is the editor's].
We'll now use indirect logic to show that (D,1) must be a ship segment. If it were water, we'd have the following forced moves leading to a contradiction:
Make (D,1) a water square: |
|
The remaining squares in column 1 must be ship segments: |
|
Column 3 must contain a cruiser: |
|
The remaining squares in row E are ship segments, creating a second (illegal) cruiser, and leading to a contradiction: |
|
Therefore, (D,1) must be a ship segment:
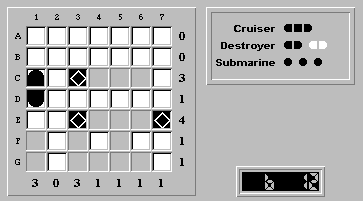
Finally, we'll solve the board by noting that there are exactly two positions to place the one cruiser:
Positioning the cruiser at (E,3)-(E,5) leads, through simple steps, to a contradiction:
Position the cruiser at (E,3) - (E,5): |
|
(C,6) is obviously a submarine: |
|
(G,3) is also a forced submarine, which leads to four submarines on the board (a contradiction -- only three are allowed): |
|
Therefore the cruiser must be positioned at (E,5) - (E,7):
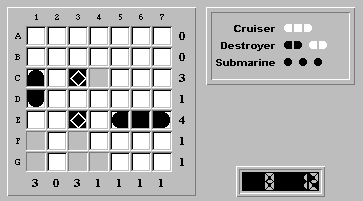
(C,4) is a forced ship segment:
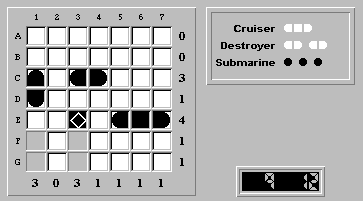
Finally, we need to place the three remaining submarines in a 3x3 area (rows E-G, columns 1-3) where one of the ship segments is known to be (E,3). This common pattern has one solution, which leads to the solution:
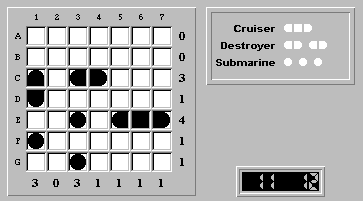
As an added bonus, we bettered the automatic solver's solution of twelve steps -- we did it in eleven!
