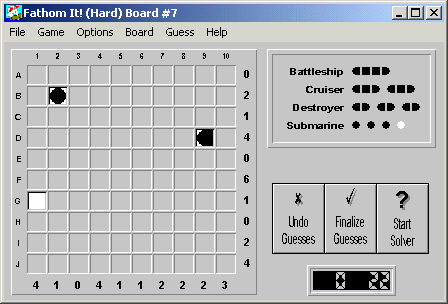
Here is the initial board:

The first step is to complete the destroyer by placing a ship segment at (D,10), filling in the obvious waters along the way:
The remaining empty cells in column 1 are obviously all ship segments:
We're going to make use of the following solving rule, formulated by Shmuel Siegel, which says the following:
"A 6x2 or 7x2 area that needs five (5) ship segments in one row and one (1) in another row must have one vertical pair of ship segments within the rectangle. In the 6x2 case the vertical pair must be on the leftmost or rightmost extremity."
(A similar rule can be formulated for 2x6 or 2x7 areas.)
Let's explain this solving rule in detail.
In the current board position, rows F and G have a rectangular area that is 7x2 squares large:
In addition, the "effective" tally (i.e., the number of segments still left to find) for row F is five (5), and the tally for row G is one (1):
So we have the necessary ingredients to apply the rule: we have a 7x2 rectangular area with an effective tally of five and one. According to the rule (which we still need to prove), there must be a vertical sequence of two segments (either a destroyer or part of a larger ship) somewhere in the rectangle. This vertical sequence will account for the single segment in the row with a tally of one.
In our current case, the rectangle is delimited by rows of water immediately above and below the rectangle, so the rule here means there is a vertical destroyer in the rectangle.
Let's see why this is true. Suppose row G's tally of one is due to a submarine. Where can we place this submarine along row G? It cannot go in any of columns 5 through 9. One such placement will suffice to demonstrate why this is true:
You can see why now: the submarine closes off too many cells in the adjacent row to enable placing the remaining five segments. So placing the submarine in any column other than the two outer cells not possible.
We also cannot place the submarine in either of the outer cells -- doing so leads to a five-segment ship:
Therefore, the row with the tally of one cannot have a submarine in it. The forced conclusion is that there is a vertical sequence of two ship segments within the rectangle.
Let's return to our board:
Using the just-formulated rule, we know that the (F,4) - (G,10) rectangle has a vertical destroyer within it. We're going to use this knowledge in a moment. In the meantime let's continue, trying to place the battleship.
The battleship can only be placed along row F. Due to overlapping positions, square (F,7) must be a ship segment:
Now we'll make use of the "7x2" rule. We know there must be a vertical destroyer in the (F,3) - (G,10) rectangle. After placing the battleship segment, there are only two positions for this destroyer within the rectangle: column 4 or column 10.
It cannot be placed in column 4:
There is no way to place the remaining two (2) cruisers! We can place at most one cruiser in row J, and row F already contains a battleship.
Therefore the vertical destroyer is in column 10:
At this point we've basically solved the board. We can add two more overlapping ship segments due to the battleship in row F:
There is only one way to place both cruisers: in (B,4) - (D,4) and in (J,7) - (J,9):
Filling the forced submarine along row I forces the battleship, giving the solution: