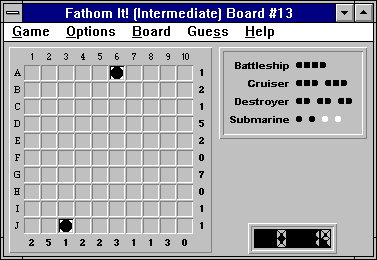
Here is the initial board:

Finalizing any obvious water square (for example (A,5)), causes Fathom It! to fill in all obvious water squares (known as smart fill). This results in:

Column 2 can be filled in with ship segments, followed by column 1:

Row G catches our eye because we have to place the five remaining ship segments in six unknown squares. Another way to look at it is that we must place the one remaining water square along row G.
The remaining water square cannot be placed in (G,4). Doing so would mean that squares (G,5)-(G,9) are ship segments, creating an illegal 5-segment ship (the longest is four). Likewise (G,9) cannot be water, resulting in a 5-segment ship. Therefore squares (G,4) and (G,9) are ship segments.
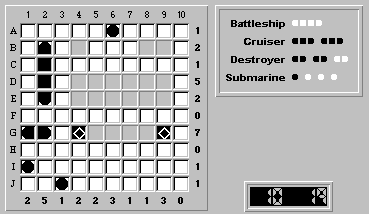
We'll now show that the squares (G,5) and (G,8) are also ship segments. Here are two different methods for proving the assertion:
First method: We can't have two battleships
If (G,5) were water, that would turn the remaining unknown squares in row G into ship segments, creating a second (illegal) battleship in (G,6)-(G,9). Similarly, setting (G,8) to water would create a second battleship at (G,4)-(G,7). Therefore, squares (G,5) and (G,8) are both ship segments.
Second Method: We can account for all the submarines
There are three visible submarines at (A,6), (I,1) and (J,3). Although we don't know the precise location of the fourth (and last) submarine, we know for certain it is in row B. This is because row B has one remaining ship segment, and that segment must be a submarine.
If (G,5) were water, that would turn (G,4) into a fifth (and illegal) submarine. Similarly, (G,8) as water would turn (G,9) into a fifth submarine. Therefore, squares (G,5) and (G,8) are ship segments.
Whichever method is used, we can finalize (G,5) and (G,8) as ship segments:

Now let's try to place the two cruisers. Checking the board tallies shows us that one cruiser must be placed along row D, and the other along row G. No matter where the cruiser is positioned along row D, the squares (D,5) and (D,6) will be ship segments.
An added benefit of placing a cruiser along row D is that (D,9) must be a ship segment. This is because row D has a tally of five, of which four segments are accounted for (the segment in (D,2) and the cruiser along row D).
Filling in the segments gives us:

Filling in the remaining ship segment in row E forces the solution of the board:
